Today's Flag Lecture
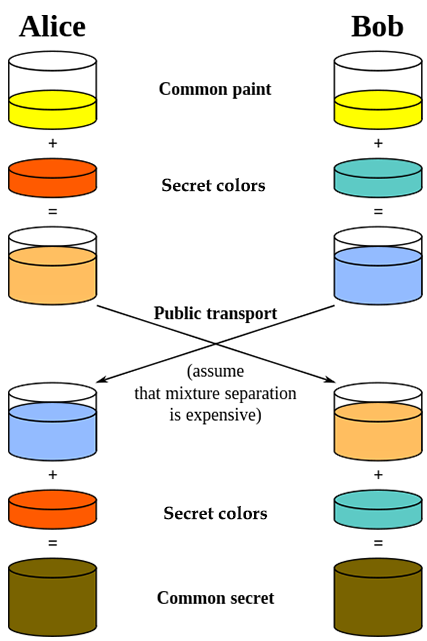
The math is basically like this pick a random \(a\) and a big prime \(p\).
Protect that little \(a\) it is your super secret private key.
Now tell the world \(A = 2^a\) mod \(p\).
Listen for your partner to tell you their \(B = 2^b\) mod \(p\).
Here's the magic: You use your \(a\) and calculate \(B^a\) mod \(p\).
How does this work? \(B^a = (2^b)^a = 2^{ab}\) but the other person
knows \(b\) and \(A=2^a\), so they calculate \(A^b = (2^a)^b = 2^{ab} \).
Little demo:
First we solve the flag, then pick a partner, and have a secret conversation in our public discord.
OK swapping keys in public:
Flaw 1: number theory needs care (backdoors included)
Play this game with me:
See the Pen
Chinese Remainder Theorem Game by Andy Novocin (@AndyNovo)
on CodePen.
This is called the Chinese Remainder Theorem, and it's pretty intuitive and clever and useful.
Here is how that undermines Diffie-Hellman:
Topic 1: Pohlig-Hellman
You have this problem to solve, given \(g, h, p\) find the unknown \(x\) such that \(g^x = h\) mod \(p\).
We know, thanks to Fermat's little Theorem, that
\(m^{p-1} = 1 \) mod \(p\) for any integer \(m\).
So we're interested in reducing the search space for \(x\) from \(1, \cdots, p-2\) to something much smaller.
The idea is that we can actually figure out \(x\) mod \(m\) for any \(m\) that divides \(p-1\)
When I go concrete I'll use \(p=31\) in the following to match the notes.
To show how that works let's play with \(x\) mod \(3\). Every integer can be written down as \(3k, 3k+1,\) or \(3k + 2\)
for an arbitrary integer \(k\). This comes from when we looked at modular
arithmetic as infinite sets, like \(3 \cdot \mathbb{Z} + 1\) as this big infinite set of all things that are 1 larger than a multiple of 3.
We don't know which of those 3 worlds \(x\) lives in but we could say that
\(x = 3k + y\) where \(y\) is either 0, 1, or 2.
At this point maybe it seems a tad abstract but if we can change this problem from hunting
for \(x\) inside the range \(1, \cdots, p-2\) to hunting for \(y\) in the range \(0,1,2\)
we've certainly made a smaller problem.
OK NOW we're ready to play with the
original equation: \(g^x = h\)
Let's replace \(x\) with \(3k + y\):
\(g^{3k + y} = h\)
We know that \(g^{p-1} = 1\). Now if 3 happens to divide \(p-1\) like in the \(p=31\) case
then we have a trick we can use:
In our \(p=31\) case Fermat's little theorem gives \(g^{30} = 1\).
So the big idea is that we can raise both sides of the main equation to the 10th power.
Watch what happens
\(g^{10 \cdot (3k + y)} = h^{10}\)
Playing with the left hand side we get:
\( g ^{10 \cdot (3k + y)} = g^{30k + 10y} = g^{30k} \cdot g^{10y} = (g^{30})^{k} \cdot g^{10y} = (1)^{k} \cdot g^{10y} = g^{10y} \)
So that means \(g^{10y} = h^{10}\)
Did we make progress?
Well now we have a simple search to do, look at \(g^0, g^{10}, g^{20}\)
and compare those 3 values with \(h^{10}\) (all of this is mod 31)
So we calculate \(h^{10}\) and compare it with the three possible values of
\(y\) and we KNOW that one of them will match up. Let's say when \(y=1\) for some
specific value of \(h\) then it must be that \(g^{10} == h^{10}\) which would imply
that \(x = 3k + 1\) for some value of \(k\). Now we know that the final answer
will be 1 mod 3.
You can imagine that we could repeat this process for other factors of \(p-1\).
When \(p=31\) that would mean 2, 3, 5.
But could the trick work for other moduli?
Like, no one is stopping us from writing down \(x = 7k + y\).
So plug it in to the original equation: \(g^x = h\)
We get \(g^{7k + y} = h\) But since 7 doesn't divide 30 we don't
have some nice way to get rid of needing to find the \(k\) AND find the \(y\).
Raising both sides to any power is never going to reduce my search space.
That is the heart of Pohlig-Hellman, for numbers \(m\) that divide \(p-1\) we can
change the search space from \(m \cdot k + y\), (where \(y = x\) mod \(m\) ), to
ignoring needing the \(k\) and only needing to find \(y\) which is ALOT less work.
After all of that use Chinese Remainder Theorem to finish the problem.
Next Lecture Flag:
Flaw 2: Man-in-the-middle attack
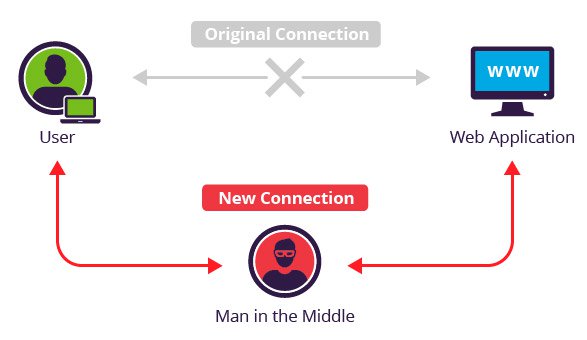
OK, so in a public-key exchange I can establish a secure connection with
anyone (up to the number theory choices/risks). BUT now identity of WHO
I am talking to becomes very important.
The most common application of this DHKE process is TLS the HTTPS protocol for
encrypting website traffic. So the act of ensuring that no one is pretending to
be a site that they are not is important.
Public Key Infrastructure
This is the idea of certs, and who signs them, and what is a digital signature.
Also the chain of trust and DNSSEC and a whole TON of work
by the IETF and Certificate Authorities and so on.

https://www.cloudflare.com/learning/ssl/how-does-ssl-work/
Friday Afternoon Fun
Look at a real certificate in Wireshark
Make a self-signed certificate at the command-line
Use let's encrypt to sign a cert automagically for a domain you own